定义

Delaunay 三角剖分是对平面有限点集P的三角剖分DT，P中的点不在任意一个DT三角形外接圆里。 它满足两个重要准则：

  1. 空圆特性。Delaunay 三角网是唯一的（任意四点不能共圆），在 Delaunay 三角形网中任一三角形的外接圆范围内不会有其它点存在。如下图：

    空圆特性

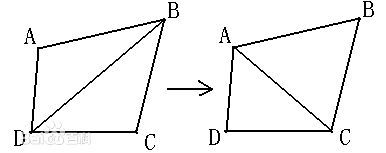
  2. 最大化最小角特性。在散点集可能形成的三角剖分中，Delaunay三角剖分所形成的三角形的最小角最大。如下图：

    最大化最小角特性

Delaunay 一词是为了纪念 Boris Delaunay 在 1934 年在这方面做的贡献。

粗略定义就是这样，Delaunay 三角剖分有一些很优异的性质：

  1. 最接近的点形成三角形
  2. 唯一性，无论何种算法，最后得到的 Delaunay 三角剖分是唯一的
  3. 最规则，由最大化最小角特性可以推出，Delaunay三角网是“最接近于规则化的”的三角网
  4. 所有三角形并集为点集的凸包（这个所有剖分都是哈 -_-b）

算法

常规算法有 Flip 算法，Incremental 算法，Divide and conquer 算法，Sweepline 算法等。

Flip 算法

Flip 算法基于一个思想，就是 Lawson 提出的局部优化过程 LOP(Local Optimization Procedure)，一般三角网经过 LOP 处理，即可确保成为 Delaunay 三角网。 LOP过程如下：

  1. 将两个具有共同边的三角形合成一个多边形。
  2. 以最大空圆准则作检查，看其第四个顶点是否在三角形的外接圆之内。
  3. 如果在，修正对角线即将对角线对调，即完成局部优化过程的处理。

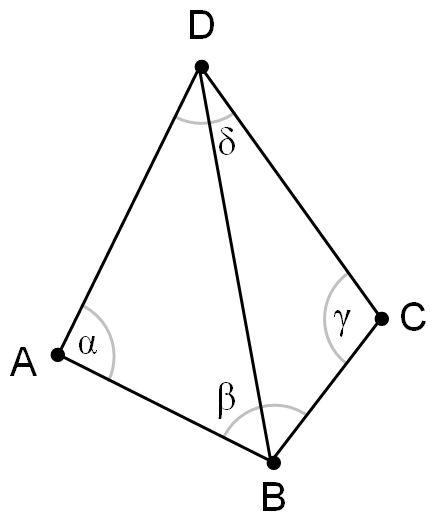
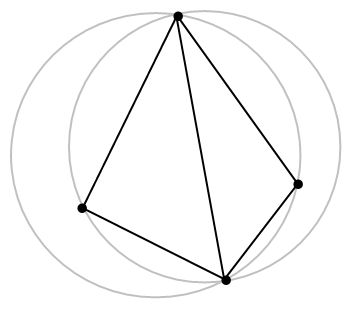
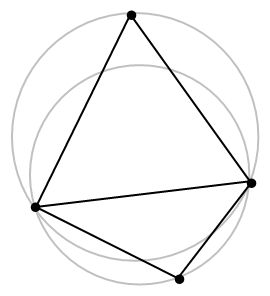
$\alpha$和$\gama$之和大于$180^\circ 不满足空圆特性 对调对角线形成 Delaunay 三角剖分

这样我们从任意一个三角剖分开始，检查非 Delaunay 边，反转边，直到符合 Delaunay 三角剖分为止。这个算法效率较差，不能推广到高维。

Incremental 算法

这不是一个算法，是一类算法。这类算法很直观，依次插入点，重新计算受影响的部分。

直接的增量算法

  1. 构造一个大三角形，包含点集
  2. 依次插入点集中的点，插入时将一个三角形分成3个，遍历所有三角形，用 LOP 过程处理非 Delaunay 三角形
  3. 最后移除第一步中插入的三个点及其所在的三角形即得结果

查找点在哪个三角形里面需要遍历所有三角形，反转也至多反转所有三角形，所以算法上限是$O(n)$。但是一般情况下，若是随机插点的话， 只有$O(1)$的三角形需要反转，故实际效率会好一点。

Bowyer–Watson 算法

该算法和上面的算法类似，只有在插点时有些不同：

  1. 构造一个大三角形，包含点集
  2. 依次插入点集中的点，去掉外接圆包含插入点的三角形，留出一个星形空洞，连结插入点和空洞边上的点，重新剖分
  3. 最后移除第一步中插入的三个点及其所在的三角形即得结果

看一个实际例子，黄色圆是受影响的三角形的外接圆：

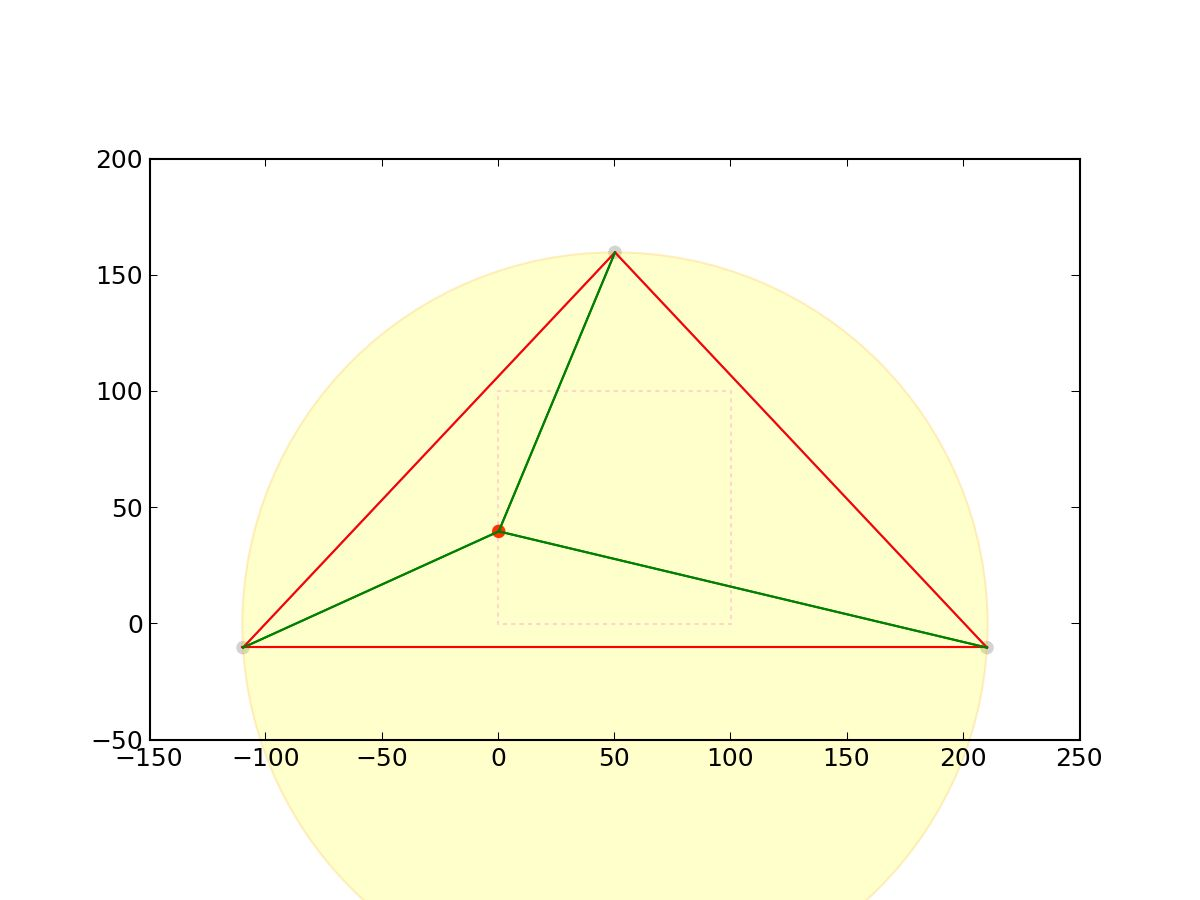
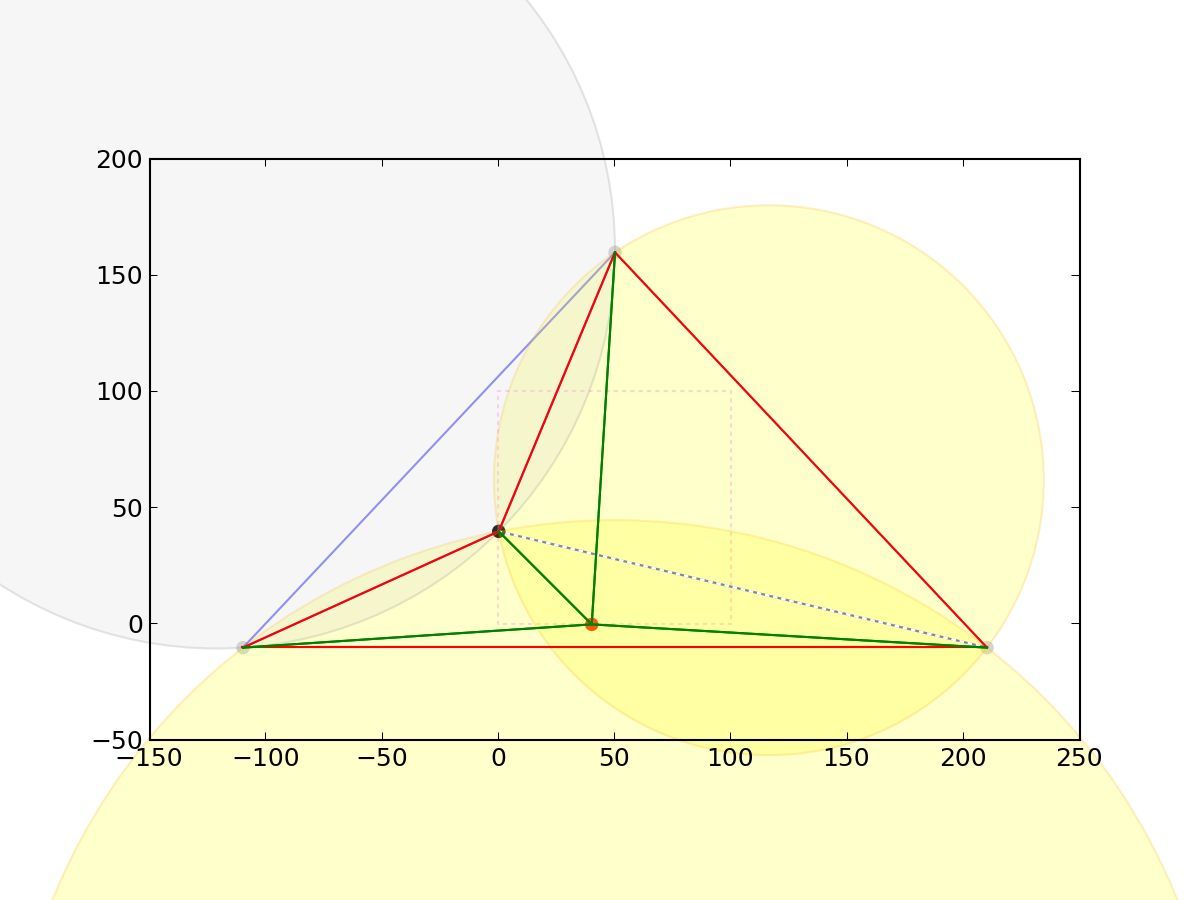
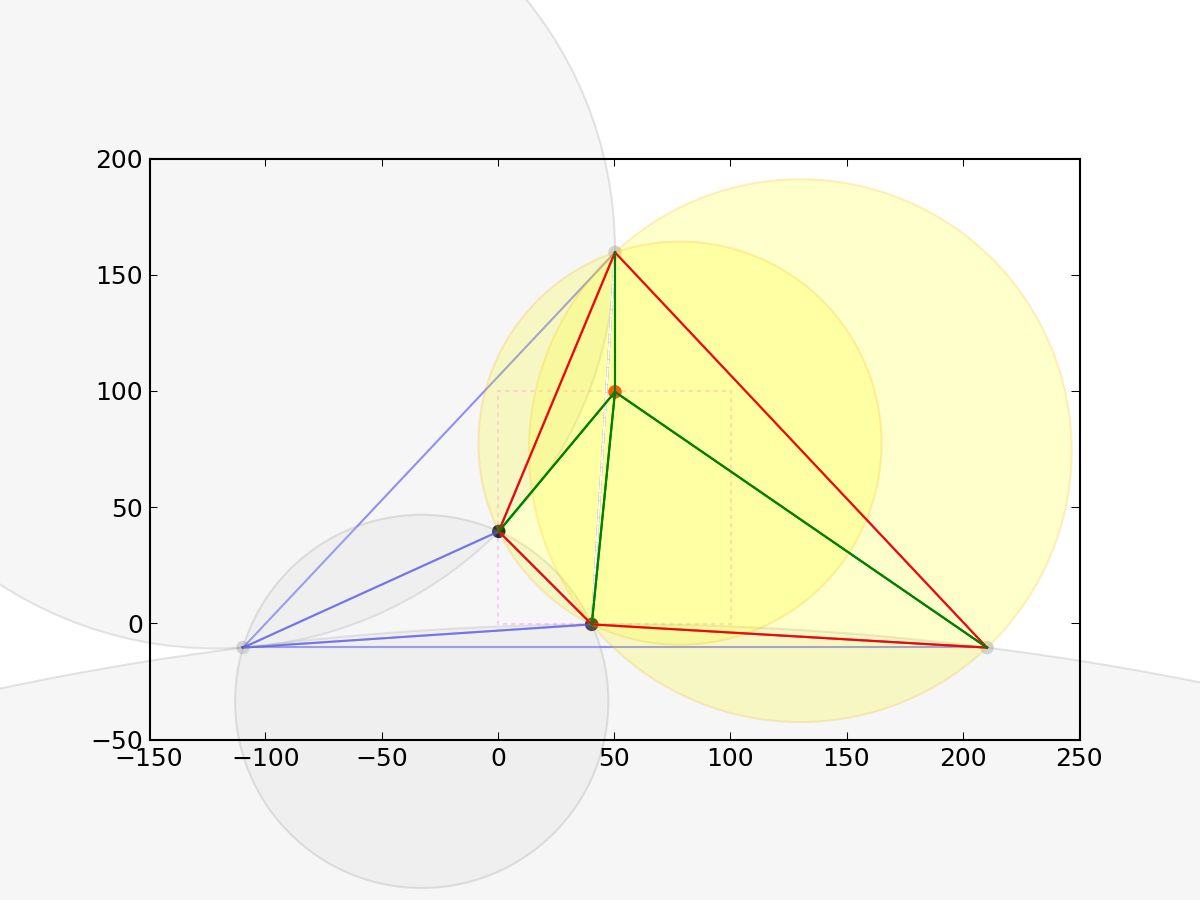
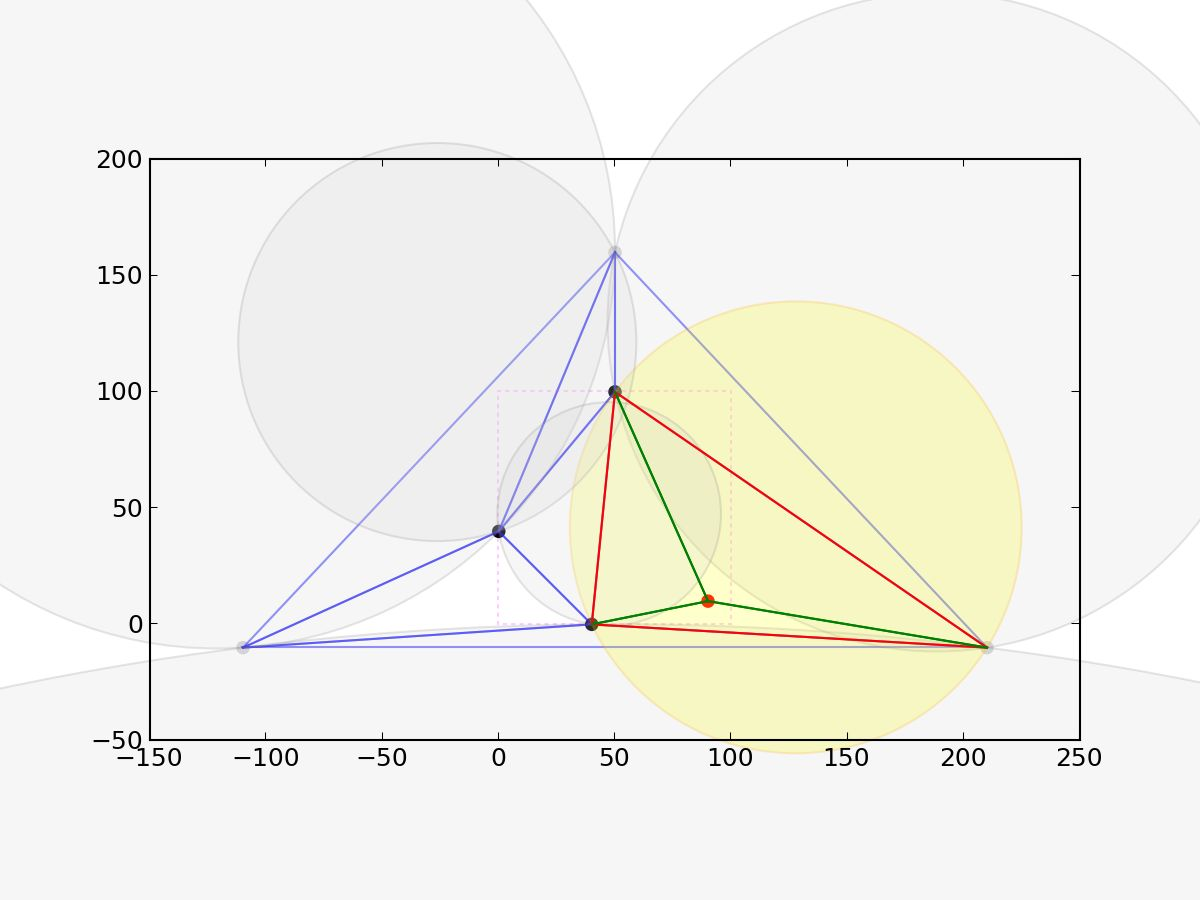
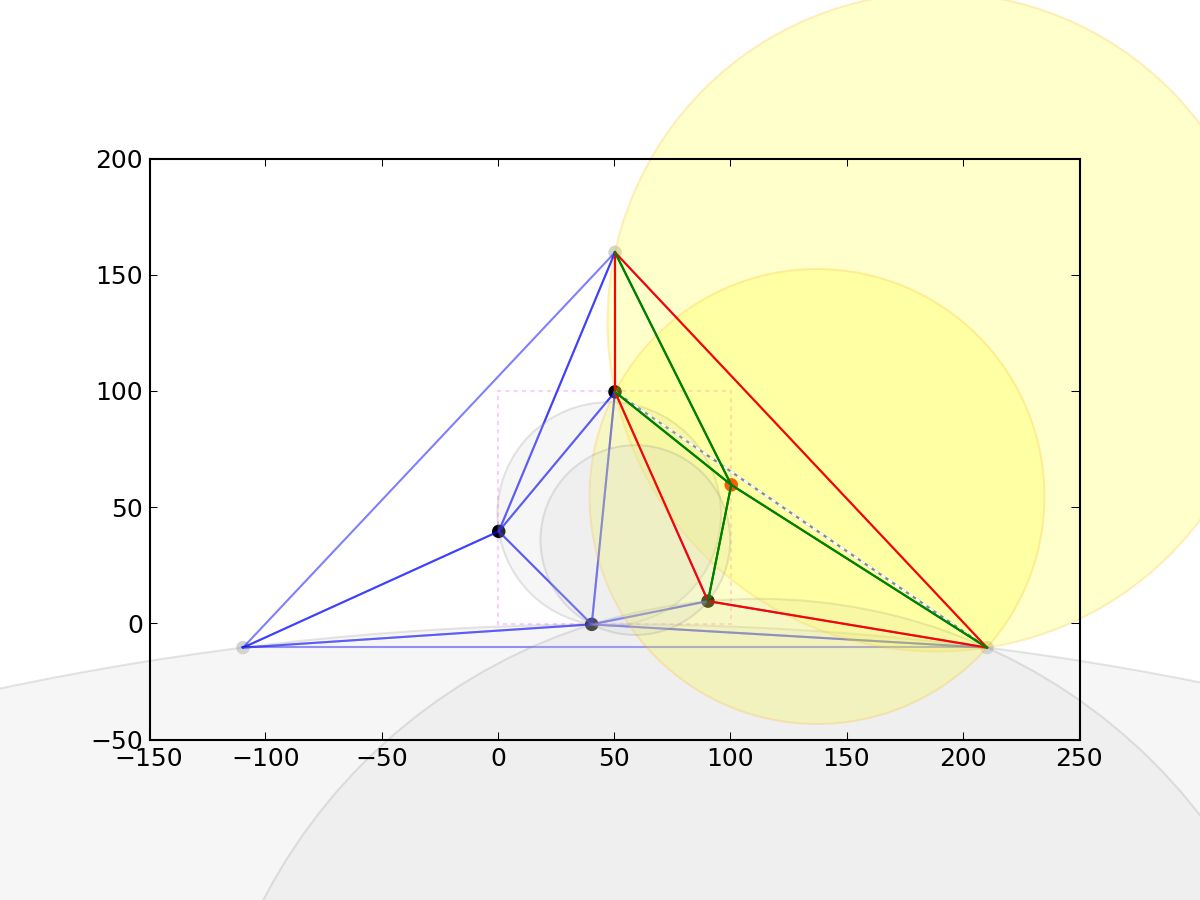
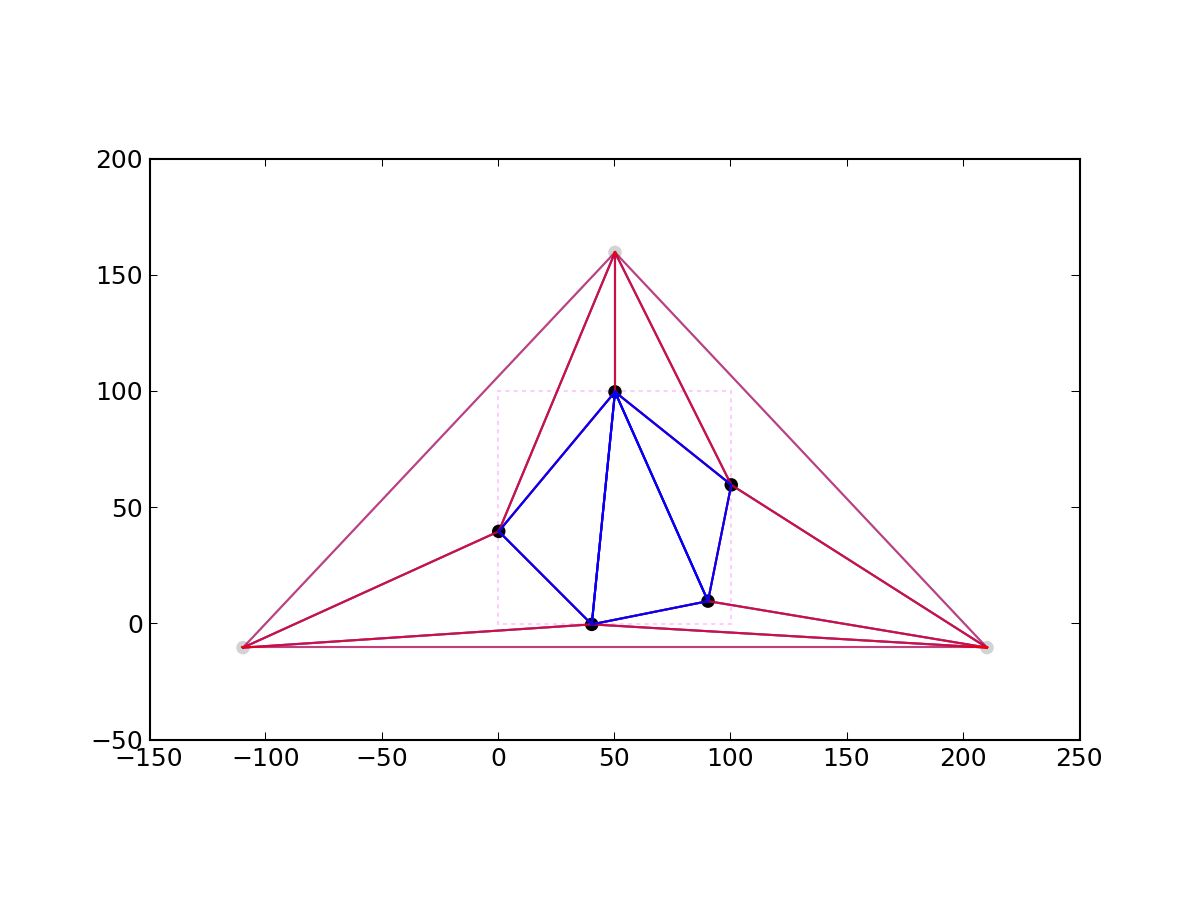
Bowyer–Watson插入第一个点 Bowyer–Watson插入第二个点 Bowyer–Watson插入第三个点 Bowyer–Watson插入第四个点 Bowyer–Watson插入第五个点 Bowyer–Watson去除超级三角形

分治法

基本思路是递归分割点集，到点很少的时候，比如3个，这个 Delaunay 剖分就是三点连线。然后把剖分结果沿分隔线合起来。 和起来的过程也可以使用 LOP 消除非 Delaunay 三角形。

有机会以后再讨论这个算法，其中 DeWall 算法是目前 Delaunay 剖分最快的算法。

Sweepline 算法

扫描线算法先将点集按某一维排序，比如$x$，然后用平行另一维的直线依次扫描点集，动态构建剖分。

结尾

二维的算法就介绍到这里，其实里面有些算法是可以推广到高维的。下次再介绍一下约束的 Delaunay 三角剖分以及三维的四面体剖分。

Computational Geometry  Delaunay triangulation